The Importance of Building Strong Relationships

Relationships play a crucial role in both our personal and professional lives. Whether it’s with family, friends, colleagues, or clients, cultivating strong relationships is essential for success and happiness.

In the business world, relationships are the foundation of success. Building strong connections with clients, partners, and colleagues can lead to increased collaboration, trust, and ultimately, better results. A positive relationship can help businesses navigate challenges, seize opportunities, and foster loyalty.

Effective communication is key to nurturing relationships. Listening attentively, showing empathy, and being responsive are all important aspects of building strong connections. By understanding the needs and perspectives of others, we can build trust and mutual respect.

Moreover, relationships are not just about what we can gain; they also bring joy and fulfilment to our lives. Connecting with others on a deeper level can provide emotional support, a sense of belonging, and a source of motivation.

It’s important to invest time and effort in building relationships. Regular communication, genuine interest in others’ well-being, and acts of kindness can all contribute to strengthening bonds. Remembering important dates or milestones for others shows that you care and value the relationship.

In conclusion, relationships are the cornerstone of a fulfilling life and successful business ventures. By prioritising communication, empathy, and mutual respect in our interactions with others, we can cultivate meaningful connections that enrich our lives and contribute to our success.

Understanding Relations in Mathematics: 7 Frequently Asked Questions

1. What is a relation in math?
2. What is the relation and relationship?
3. What do you mean relation?
4. What is a relation and give one example?
5. What do you mean by relation?
6. What is meant relation example?
7. Is a function a relation?

What is a relation in math?

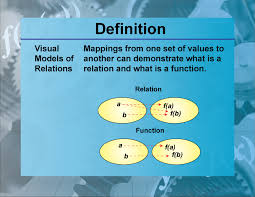
In mathematics, a relation refers to a set of ordered pairs that establish a connection between elements from two sets. Essentially, it defines how elements from one set relate to elements in another set. Relations can be represented graphically, algebraically, or through tables, and they play a fundamental role in various mathematical concepts such as functions, equivalence relations, and mappings. Understanding relations is crucial in analysing and describing the relationships between different mathematical entities, providing a framework for solving problems and making connections within the field of mathematics.

What is the relation and relationship?

The terms “relation” and “relationship” are often used interchangeably, but they have distinct meanings. A relation typically refers to a connection or association between two or more things, such as cause and effect, similarity, or interaction. On the other hand, a relationship usually implies a deeper and more personal connection between individuals or entities. Relationships involve emotions, trust, communication, and mutual understanding, often forming the basis for meaningful connections in both personal and professional contexts. While relations can be more general and abstract, relationships tend to be more specific and intimate, playing a significant role in shaping our interactions with others.

What do you mean relation?

In the context of human interactions and connections, the term “relation” refers to the way individuals or entities are connected to each other through various forms of association, such as familial ties, friendships, professional networks, or business partnerships. Relations encompass the dynamics of communication, trust, mutual understanding, and shared experiences that shape the bond between people or organisations. Building and nurturing positive relations is essential for fostering collaboration, support, and a sense of belonging in both personal and professional settings.

What is a relation and give one example?

A relation refers to the connection or association between two or more elements, often based on a specific criteria or characteristic. In mathematics, a relation is a set of ordered pairs that establish a relationship between elements of different sets. For example, consider the relation “is taller than” between individuals in a group. If we have individuals A and B, and A is taller than B, this establishes a relation where A is related to B based on their height comparison. This simple example illustrates how relations help define connections and comparisons between different entities.

What do you mean by relation?

In the context of interpersonal connections and communication, a relation refers to the way individuals or entities are connected or associated with each other. It encompasses the dynamics, interactions, and bonds that exist between people, whether in personal relationships, professional settings, or broader social contexts. Building positive relations involves fostering understanding, trust, and mutual respect to create meaningful connections that can lead to collaboration, support, and shared experiences.

What is meant relation example?

In the context of relationships, a common question often asked is, “What is meant by relation example?” When we refer to a relation example, we are typically seeking a specific instance or scenario that illustrates the concept of relationships in a tangible way. For instance, a relation example could be a situation where effective communication and mutual understanding between colleagues lead to successful collaboration on a project, highlighting the importance of building strong relationships in achieving common goals. Such examples help to clarify and demonstrate the significance of relationships in various contexts and how they impact our interactions and outcomes.

Is a function a relation?

In mathematics, a function is indeed a type of relation. Specifically, a function is a relation between two sets in which each element of the first set is associated with exactly one element of the second set. This unique mapping distinguishes functions from general relations, which may have multiple outputs for a given input. Functions are fundamental in mathematics and are used to describe many real-world phenomena and relationships between variables.